Intermediate Formal Logic and AI (= IFLAI2) Fall 2022 edition of IFLAI2 Selmer Bringsjord
Table of Contents
Selmer Bringsjord
with Naveen Sundar G. \(\wedge\) …
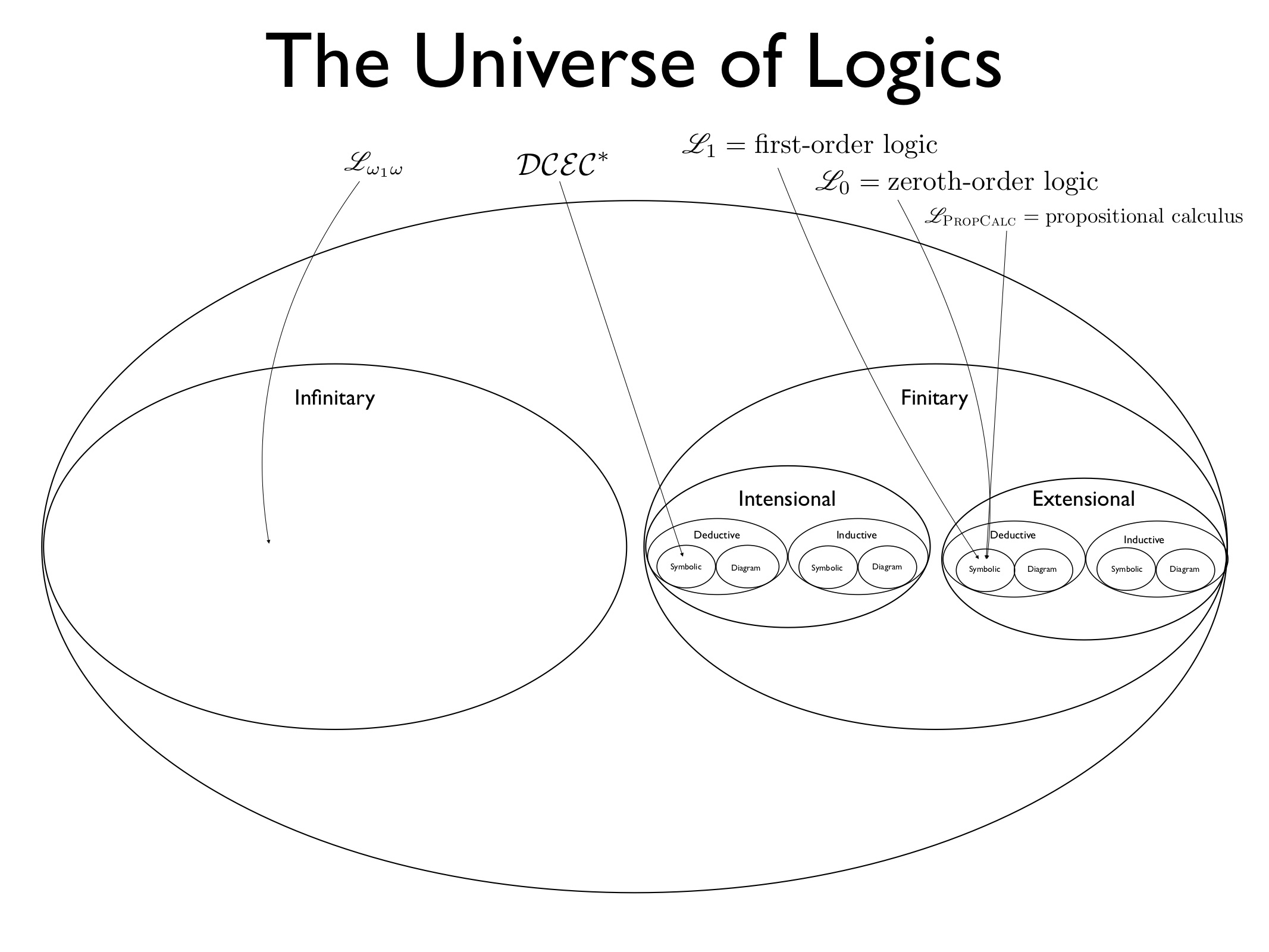

Figure 2: Larry

Figure 3: Lucy
[All artwork (all of which is copyrighted) for the LAMA paradigm by KB Foushée.]
General Orientation
This course gives advanced, accelerated coverage of intermediate formal logic and logic-based (= logicist) AI. The course makes crucial use of AI for learning, and also provides coverage of selected “big questions” in and arising from logicist (= logic-based) AI. In addition, students are exposed to a pure and general form of logic programming, so-called Pure General Logic Programming (PGLP), and will be able to themselves write not only proofs, but proofs that include functional code written in Clojure, in the new logic-programming language HyperLog®.
- What is Formal Logic?
In general, formal logic is the science and engineering of reasoning,1 but even this supremely general description fails to convey the flexibility and enormity of the field. For example, all of classical mathematics can be deductively derived from a small set of formulae (e.g., ZFC set theory, which you’ll be hearing more about, and exploring) expressed in the particular formal logic known as `first-order logic’ (FOL = \(\mathscr{L}_1\), which you’ll also be hearing more about), and computer science emerged from and is in large part based upon logic (for peerlessly cogent yet non-technical coverage of this emergence, see C Glymour’s Thinking Things Through). Logic is indeed the foundation for all at once rational-and-rigorous intellectual pursuits. (If you can find a counter-example, i.e. such a pursuit that doesn’t directly and crucially partake of logic, S Bringsjord would be very interested to see it.)
- Context: A Research University
You have wisely decided to attend a technical research university, with a faculty-led mission to create new knowledge and technology in collaboration with students. RPI is the oldest such place in the English-speaking world; it may know a thing or two about this mission. The mission drives those who teach you in this class. The last thing we want to do is simply convey to you how others present and teach introductory formal logic. As should be obvious by now, we think we have invented a better way to define, specify, and present formal logic, and are working hard to explain this invention, to explain it to others, and to disseminate the invention in question. The better way in question is denoted by the phrase ‘Logic: A Modern Approach®,’ or simply by the abbreviation ‘LAMA®,’ pronounced so as to rhyme with ‘llama.’
- A Disclaimer!
Please note that guest lecturers other than NS Govindarajulu and A Bringsjord should not be assumed to have fully affirmed the LAMA® paradigm.
As to what these thinkers hold in connection with LAMA®, that is an open question. You are free to inquire!
- Prerequisites
Students must have had a previous, rigorous, comprehensive course in formal logic. It is highly beneficial that the student have had in this prior course, or from some other source, modal logic. Realistically, some students will have only studied mathematical logic or standard extensional logics in their prior coursework. There is nothing to be done about this save to inlude early on some coverage of modal logic via independent work by the student in HyperSlate® on some modal-logic problems.
Texts/Readings
First, students new to AI should read this overview of the field.
Next, students will purchase access to and obtain the symbiotically interconnected trio of
- the e-text Logic: A Modern Approach; Beginning Deductive Logic via HyperGrader® and HyperSlate®, Advanced (LAMA-BDLHGHSA);
- the HyperSlate® interactive AI-infused environment for (among other things) proof and program construction in collaboration with AI technology (= the “oralces”); and
- HyperGrader®, an AI-infused online platform for assessing student progress (HG® comprises HS®)
published by Motalen. Each member of this trio will be available online after purchase of a license, via the relevant code-carrying envelope in the RPI Bookstore. Full logistics of this purchase, and the content of the envelope and how to proceed from this content, will be explained the first class (and subsequently, as needed). Updates to LAMA-BDLHGHSA, and additional exercises, will be provided by listing on relevant HyperGrader® web pages upon signing in (and sometimes by email) through the course of the semester. You will need to manage many electronic files in this course, and e-housekeeping and e-orderliness are of paramount importance. You will specifically need to assemble a library in HyperGrader® of completed and partially completed proofs and other files in so that you can use them as building blocks in harder proofs; in other words, building up your own “logical library” will be crucial.
Please note that HyperGrader® and HyperSlate® are each copyrighted, trademarked, and Pat. Pend.: copying and/or distributing this software to others is strictly prohibited. You will be asked to AGREE online after the time of registration to a License Agreement. This agreement will also cover the etextbook, which is copyrighted as well, and cannot be copied or distributed in any way, even in part.
In addition, occasionally papers will be assigned as reading.
Finally, slide decks used in class will contain crucial additional content above and beyond LAMA-BDLHGHSA, information posted on HyperGrader®, and in your library for HyperSlate®; this additional content will be available on the web site as the course unfolds through time.
Syllabus
The version of the course now underway is the Fall 2022 edition, the syllabus for which is available here. This is a robust, detailed syllabus, and is required reading — and reading that will pay off, for sure.
HyperSlate®
This is the interactive environemnt system used for constructing proofs and arguments, and — in HyperLog® — pure logic programs (Clojure functions to make function symbols in formulae “live”), in collaboration with AI technology (our “oracles”), and is available here after registering, agreeing to the license agreement, and signing into HyperGrader®.
HyperGrader®
This is Motalen’s overarching AI platform for submitting, getting assessed, and earning trophies and learderboard points for proofs, arguments, and — in HyperLog® — pure logic programs (along with Clojure functions to make function symbols “live”) constructed in HyperSlate®, and is available here after registration and by sign-in.
LAMA-BDLHGHSA Textbook
This is the e-textbook for the course, and is obtained after registration and sign-in to HyperGrader®, via download. New versions of the book will appear directly in HyperGrader® for download.
Class-Day Topic and Content (includes associated slide decks, video lectures, and — sometimes — tutorials, etc.)
Please note that for some classes there will be a slide deck and a video lecture (but the video lecture often will not be posted until after synchronous in-person instruction, and in some cases may not be posted, in order to prevent certain data from being fully public).
- August 29 2022: General Orientation to the LAMA® Paradigm, Logistics, Mechanics (S Bringsjord)
The syllabus was projected and presented, and discussed, in detail. Please note that the syllabus, in particular, makes clear that students who wish to opt learning under a different paradigm than that of LAMA® should take “straight” Intermediate Logic from another instructor, since probably the “Stanford paradigm” is in use then, and in that case the course will not be based upon or cover AI and AI-based topics, and will not be based on Motalen’s technology.
- September 1 2022: Tutorial, Mechanics; Historical and Scientific Context re. Formal Logic, AI, and Logic Machines (S Bringsjord)
We begin by considering, armed with formal logic, the question “What is school for?,” taken up today (9/1/22) in a symposium hosted by the New York Times. Then, after a brief review of some course mechanics, we remind students that prowess in cracking problems in \(\mathscr{L}_{PC}\), \(\mathscr{L}_1\), and \(\mathscr{L}_2\) is assumed, and may need to be refreshed. (A problem for each logic will be posted on HyperGrader®; on about Sept 12.)
We then take a time-traveling tour of computational formal logic and AI, going from Euclid, three centuries BC, to — possibly? — The Singularity in our future, and put some ephasis on the Entscheidungsproblem. The final phase of this session has a focus on form of AI and computer programming based on formal logic: viz. “The Terrific Triad” of circa 1965, resurrected, refined, and reenergized.
- A (past) Corresponding Video Lecture by S Bringsjord, “The Terrific Triad,” is available here.
- September 6 2022: Review of Extensional Logics (contrasted with intensional logics) (S Bringsjord)
In this pre-recorded lecture, available here, we use the case of Blinky (Lost in Space) to explain the core difference between extensional versus intensional logics. (Later in the class we shall employ the infinitary version of the False Belief Task to further display what’s unreachable for extensional logics, and why.) We end by returning to the extensional trio of \(\mathscr{L}_{PC}\), \(\mathscr{L}_1\), and \(\mathscr{L}_2\). In the second of these extensional logics, and using our AI oracles in HG®, we first explore an example from 1957 by Layman Allen, who dreamed of formal logic capturing the U.S. tax code, and then explore
SpecialLlamasDisjunction, introduced in our previous meeting. We end with coverage of \(\mathscr{L}_2\), second-order logic, and the so-called \(k\)-order ladder.- Recommended Reading (for contrast, and to set up for our next class): “Intensional Logic” in SEP
- September 8 2022: Review of/Entry to Intensional/Modal Logics (S Bringsjord)
This too is a (substantive!) pre-recorded lecture, available here. We first briefly inquire as to whether there are any questions about the \(k\)-order logic ladder, and then return to the case of Blinky (of Lost in Space fame) to begin to probe relevant s-expressions in modal logic in HS®. Next, we look at the most demanding versions of the False Belief Task that anyone in AI and/or computational CogSci has attempted; this coverage includes even the infinitary FBT. Handling these taks requires, certainly, intensional/modal logics. Finally, we encapsulate the modal logics K, T, D, 4, and 5, and focus a bit on D, an early deontic logic, in connection with Chisholm’s Paradox.
- Recommended Reading #1: “Deontic Logic” in SEP
- Recommended Reading #2: “Intensional Logic” in SEP
- September 12 2022: Church’s Theorem (S Bringsjord, w Naveen Sundar G on Turing machines)
We first have a sustained tutorial on HyperGrader® and HyperSlate®. We then present and prove Church’s Theorem, which says that the Entscheidungsproblem is unsolvable by Turing-level machines; i.e. that theoremhood in \(\mathscr{L}_1\) = FOL is Turing-unsolvable.
- Recommended Background Reading: “Turing Machines” in SEP
- September 15 2022: Completeness Theorems (S Bringsjord)
After a tutorial on “channeling Euclid” to crack some fascinating proof challenges created in homage to cognitive scientist Lance Rips, we begin with an overview of Gödel’s Great Theorems, and then pass directly to coverage the first of these theorems: the completeness theorem for \(\mathscr{L}_1\), which was the heart of Gödel’s dissertation. Our coverage here includes a characterization of completeness in general, and then in specific terms for \(\mathscr{L}_1\). We end with some remarks about Leon Henkin, well known for devising a simpler, smoother proof of the completeness theorem.
- September 19 2022: Gödel’s First Incompleteness Theorem (S Bringsjord)
We here cover the second of Gödel’s great theorems, the one that has been most discussed and revered among those he obtained: viz., his first incompleteness theorem (G1), taking at its core Peano Arithmetic (PA). After first making sure that we have a handle on PA via exploration of it in HyperSlate®, we visit a Bringsjordian proof-oriented version of the Liar Paradox, then get clear on Gödel Numbering by simply taking note of how standard dictionaries work, and then we prove the theorem. We end by considering “astrologic” in connection with Goodstein’s Theorem, which is an example the kind of mysterious arithmetic sentences that Gödel showed in G1 must exist.
- September 22 2022: Gödel’s Second Incompleteness Theorem (S Bringsjord)
We here cover Gödel’s second incompleteness theorem (G2), which is a corollary of G1 (Gödel didn’t bother to prove it directly in his proof of G1). Bringsjord first sets the stage, and then summarizes a tragic case study (formerly presented by Mike Giancola) in which inconsistency brings a jet crashing to the ground, killing both pilot and co-pilot (Giancola’s slide deck is available here). Then Bringsjord returns to the main thread, and G2 is proved.
- September 26 2022: Gödel’s Speedup Theorem (S Bringsjord)
We introduce different levels of acceleration, from fast cars (such as electric ones from Tesla and Lucid) to the space shuttle to light-gas guns from NASA to the Ackermann Function to the beyond-recursive speedup of Rado’s \(\Sigma\) (= “Busy Beaver”) function. Then we explain and prove that moving from one logic to a more expressive one can secure speedup that, like \(\Sigma\), gives non-recursive acceleration! This is Gödel’s Speedup Theorem, the engineering consequences of which (inquisitive and wise) modern minds are still sorting out.
- September 29 2022: Formal Logic, AI, Computer Science, and the Immaterial (S Bringsjord)
Formal logic, AI, and computer science all at least appear to entail some non-physical things (e.g. algorithms, infinite cardinal numbers, etc.) exist. Does the entailment go through? And if it does, does this in turn entail that we are immaterial as well? Affirmative answers to both questions are defended by Bringsjord, based directly on this forthcoming paper.
- October 3 2022: AI, Consciousness, and Lambda (\(\Lambda\)) (S Bringsjord)
This class is based on work by Bringsjord \& Govindarajulu as set out in this paper (which you should study first), and this second one, in which a new theory of machine consciousness is set out and associated with a scheme (\(\Lambda\)) for measuring this consciousness. B\&G also here articulate and analyze purported refutations of the Integrated Information Theory of consciousness advanced by Tononi \& Koch, and its associated scheme (\(\Phi\)) for measuring consciousness. In addition, it is explained how the concept of \textit{cognitive intelligence} can be based upon \(\Lambda\), and how this has substantive bearing on artificial \emph{general} intelligence = AGI.
- Zoom-mtg Info here:
Zoom meeting has expired.
- October 6 2022: Machine-Learning Machines Don’t Learn; AI Needs … Real Learning (\(\mathcal{RL}\)) in the Form of Learning Ex Nihilo (S Bringsjord)
AI of today has given the world so-called “machine learning,” or just ‘ML’ for short. But do machines doing ML actually learn? A negative answer is given, and defended; and a genuine form of learning (for natural and artificial agents), \(\mathcal{RL}\), is introduced and defended. The negative answer is based on (indeed can be found in) “Do Machine-Learning Machines Learn?”. The kind of deep, genuinely human-level learning that AI should be based on is Learning Ex Nihilo, introduced in this paper.
- Zoom-mtg Info here:
Zoom meeting has expired.
- October 10 2022 No class: Columbus Day. (Why do we not celebrate Leiv Eiriksson Day?!)
- October 13 2022: What is Formal Inductive Logic? (S Bringsjord)
This class includes compressed coverage of so-called “pure inductive logic” (PIL, as it’s abbreviated), which has become nearly the sole province of mathematicians and logicians, with AI activity nearly zero. Why? One reason, which we find compelling, is that PIL is devoid of proofs and arguments built on the basis of the formal structures involved. We use coin flips before the start of Superbowls, and the “Grue Paradox,” to help explain matters, and we consider two argument schemata (one used in a Bringsjord-Licato paper to argue that cyberwarfare is fundamentally new over and above kinetic warfare, and one used to this day in “Wigmorean” reasoning about whether a suspect/person of interest is guilty).
- October 17 2022: From the Lottery Paradox to Defeasible/Nonmonotonic Logic and AI (S Bringsjord)
We present and examine The Lottery Paradox as a portal to argument-based defeasible (= nonmonotonic) logic. We also consider the suppression task. Such logic is way to do inductive logic, including automated inductive logic, that is superior to PIL and anything based upon it or aligned with it. As an added bonus, we use the inductive logic of Selmer, Naveen et al. to solve the St Petersburg Paradox; that solution is available here.
- October 20 2022: AI to Surmount Arrow’s (Impossibility) Theorem and Adjudicate Military Decision-Making (S Bringsjord)
S Bringsjord presents the 2021 paper
“Automated Argument Adjudication to Solve Ethical Problems in Multi-Agent Environments” Bringsjord, S., Govindarajulu, N.S. & Giancola, M. https://www.degruyter.com/document/doi/10.1515/pjbr-2021-0009/pdf
as AI science & technology able to prevent such things as this tragedy, by surmounting Arrow’s Theorem.
- October 24 2022: The Argument for God’s Existence from AI (S Bringsjord)
A novel argument for God’s existence, published in this (preprint) paper, is given. This argument makes use of the concepts of the cognitive power (fleshed out in terms of formal logic) sufficient for hunting and gathering etc. in our forebears, at the level of AI as currently logico-mathematically defined in the the field itself (witness e.g. its textbooks), and needed for creating and using the branch of mathematics known as analysis.
- October 27 2022: What are We, Rigorously Speaking? (S Bringsjord)
What are we? What are our brains? (The idea here, in keeping with the nature of both formal logic and AI, is that such questions are to be answered in formal, computational terms.) Prof Richard Granger eloquently and rigorously defends an answer to these questions that is directly at odds with the answer to them given by S Bringsjord. This class immediately grounds this clash by reference to opposing papers in Theoretical Computer Science, one by Bringsjord, and one by Granger.
- October 31 2022: Logic, AI, and Tax Technology (S Bringsjord)
Selmer claims that a series of problems in the intersection of logic, AI, and taxation compose a set that is AI-complete. The discussion is anchored to a simple scenario, S, in which three agents must in some fashion have their incomes taxed in order to defend against a malicious invader.
- November 3 2022: Pure General Logic Programming (PGLP) (S Bringsjord)
The new logic-programming paradigm, Pure General Logic Programming (PGLP), invented by Selmer under support from ANR, AFOSR, and ONR, is here introduced and explained. PGLP subsumes Prolog and all its low-expressivity cousins, and renders program verification essentially effortless because (i) programs are specifications, and (ii) the verification of what is returned after execution consists simply in the checking of the proof of what is returned.
- A Corresponding Video Lecture (from the past but given Selmer’s away it will do) is here.
- November 7 2022: Introducing HyperLog (v .75) (S Bringsjord)
After informing the audience that there are in fact some proposals for computing over the reals, with associated hierarchies, the new programming language HyperLog is introduced. This introduction includes, first, a sweeping overview of the history of formal logic and varous programming languages and their roots, and then passes to the mechanics of getting started in HyperLog, by defining Clojure functions, making inferences that compute relative to those defined functions, and employing a new oracle that can at once reason at the level of first-order logic and compute Clojure-defined functions.
- November 10 2022: On Quantificational Modal Logic (S5-centric) (S Bringsjord)
We begin by recalling why we need intensional logic in the first place, with some help from “Blinky,” of Lost in Space Fame. Then we zero in on propositional S5, take note of its elegance and economy (in light of e.g. the reduction principles it caps off). Finally, we consider a first version of quantificational S5, and end with a look at the notorious Barcan Formula, which it so happens is welcomed by S Bringsjord in his modal argument for *P=NP$, available here.
- November 14 2022: Killer Robots & The PAID Problem in Star Trek TOS, D, and Beyond to DCEC* (in HyperSlate®) (S Bringsjord)
We note The PAID Problem, in a nutshell that powerful, autonomous, intelligent machines are extremely dangerous, and might well eventually destroy us, unless The Four Steps are followed. We turn to Star Trek TOS to see this dynamic in action. We specifically note that the formal computational logic to be used in The Four Steps can’t be the deficient logic D or any of its cousins — but the /Deontic Cognitive Event Calculus/* (/DCEC/*) is instead the thing to use.
- November 17 2022: DDE (Doctrine of Double Effect) => DDE* (with self-sacrifice) => DTripleE (S Bringsjord)
To start, we return to the Doctrine of Double Effect (DDE), used by Naveen Sundar Govindarajulu (NSG) and S Bringsjord to ensure that AIs (in relevant contexts) do the ethically correct thing, as shown in this IJCAI paper. It’s then explained that NSG discovered that DDE doesn’t work when the agent intending to save the day intends to do so via self-sacrifice; the new version of DDE, set out and explained in this paper, is then presented. Finally, the listener is invited to read about this Doctrine of Triple Effect in this paper, so that future discussion and debate will be possible.
- November 21 2022: Gödel’s Silver Blaze Theorem, Part I: Further Context and Proof Sketch
In order to understand Gödel’s Greatest Theorem, which — for reasons to be explained — we shall regard to be “The Silver Blaze Theorem,”, we need to have a firm understanding of axiomatic set theory, in the form, specifically, of ZFC. This session provides this understanding, and ends with a pointer to Cantor’s proof that the power-set operation, applied to the natural numbers, yields an even-larger set. This proof is also key to understanding The Silver Blaze Theorem. (All student should read the mystery story in question.)
- * November 24 2022: Thanksgiving!
- November 28 2021: Gödel’s Silver Blaze Theorem, Part II: Further Context and Proof Sketch (S Bringsjord)
In Part II of our coverage of Gödel’s Greatest Theorem, we begin in earnest by watching two videos of proofs by truth-trees in HyperSlate®, in order to establish non-entailment. Next, without making any use of transfinite numbers, we set out and reflect upon both the Continuum Hypothesis (CH) and the Generalized Continuum Hypothesis (GCH). We then analyze the reasoning of Sherlock Holmes in the The Adventure of Silver Blaze, which is fundamentally a proof of non-entailment in its own right (and shows Scotland Yard, once again, to be, well, not exactly a place of ingenious detection). Finally, we pass to presentation and explanation of a single-slide! proof-sketch of Gödel’s stunning result.
- December 1 2022: Gödel’s Time Travel Theorem (S Bringsjord)
We here look at the context, paradoxes related to and arising from, and diagrammatic justification for: Gödel’s birthday present to Einstein: a proof that backwards (forward is of course trivial) time travel in (Einstein’s) General Theory of Relativity is possible.
- December 5 2022: Should It Be Illegal to Mistreat Cognitively Conscious Robots? (S Bringsjord)
In a bit of a changeup, Selmer presents his new and soon-to-be-published argument for an affirmative answer to this question.
- December 8 2022: Could a Finite Machine Every Match Gödel? (S Bringsjord)
We make first a few brief remarks regarding the “God Theorem” of Gödel, which end with a pointer to a better route to formalize the concept of a positive property than that taken by Gödel himself (and better as well, Selmer claims, than some others who have come after). We then answer the driving question by turning to games and game-playing, and offer an overview of the game Gödel played, which is Turing-undecidable. Finally, we look (from a high-altitude point of view) at Selmer’s quartet of arguments for the proposition, contra Rapaport’s optimism, that AI will never match, let alone exceed, human intelligence.
Tutorials
- Double Existential Elim and Exportation of Absurdity (Oct 2022)
This tutorial show a double existential-elim proof, combined with exportation of absurdity/falsum.
- Getting off the Ground into HyperGrader® and HyperSlate® (Aug 2020)
This short, simple “blast-from-the-past” tutorial explains how to register if you purchased a code from a collegiate bookstore, and then includes solving a very simple proof challenge (show that if you’re given a conjunction you can deduce in HS® that \(\psi \wedge \phi\)).
- Special Llamas Disjunction (GUI pointers & use of FOL AI/oracle) (Sep 9 2020)
Another old but still perfectly informative (even in 2022’s version of HyperSlate®) little video, featuring a variant of puzzle in FOL that makes a good review problem for students coming to this class having taken their first formal-logic class a while back.
Informal Exercises and Metalogical Homeworks
These are assigned and discussed by direct point-to-point communication in in-person class meetings, and by email.
Footnotes:
Warning: Increasingly, the term ‘reasoning’ is used by some who don’t really do anything related to reasoning, as traditionally understood, to nonetheless label what they do. Fortunately, it’s easy to verify that some reasoning is that which is covered by formal logic: If the reasoning is explicit; links declarative statements or formulae together via explicit, abstract reasoning schemata or rules of inference (giving rise to at least explicit arguments, and often proofs); is surveyable and inspectable, and ultimately machine-checkable; then the reasoning in question is what formal logic is the science and engineering of. (An immediate consequence of the characteristics just listed is that AIs based on artificial neural networks don’t reason, ever.) In order to characterize /in/formal logic, one can remove from the previous sentence the requirements that the links must conform to explicit reasoning schemata or rules of inference, and machine-checkability. It follows that so-called informal logic would revolve around arguments, but not proofs. An excellent overview of informal logic, which will be completely ignored in this class, is provided in “Informal Logic” in the Stanford Encyclopedia of Philosophy. In this article, it’s made clear that, yes, informal logic concentrates on the nature and uses of argument.