Introduction to (Formal) Logic (and AI) Selmer Bringsjord
Table of Contents
with Naveen Sundar G.
\(\wedge\) KB Foushée \(\wedge\) Joshua Taylor \(\wedge\) \(\ldots\)
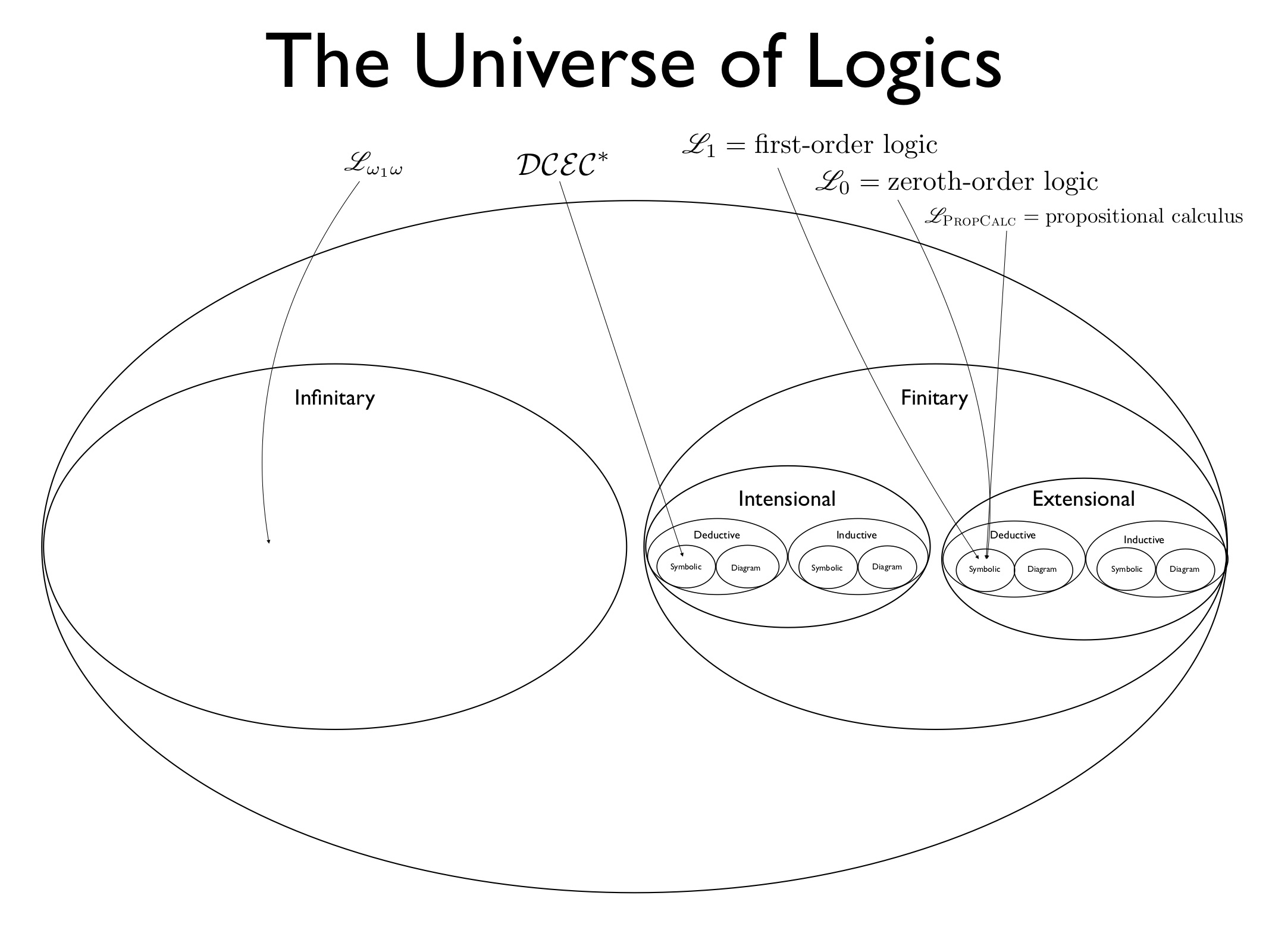

Figure 2: Larry

Figure 3: Lucy
[All artwork (all of which is copyrighted) for the LAMATM paradigm by KB Foushée.]
Terminology & General Orientation
This course is an advanced, accelerated introduction to deductive formal logic, with some substantive coverage of inductive formal logic, in which formalisms for dealing with uncertainty (e.g. probability theory, and also the likelihood calculus) are included, and to heterogeneous formal logic (which allows reasoning over not only textual/linguistic content, but visual content as well). The course conforms to the LAMATM paradigm in general, and is specifically based on Hyperlogic, which among other things (all of which are explained and covered) is based on the view that proofs and arguments are best cast as hypergraphs. Since the present course is focused on deduction, the course is specifically based on hypergraphical natural deduction. To our knowledge, this is the only robust treatment of formal logic based on this form of deduction, which as many unique advantages.
The course makes crucial use of AI for learning, and also provides an introduction to AI itself, at least AI of the logicist variety. In particular, students are exposed to a pure and general form of logic programming (so-called PGLP) that is particularly well-suited for pursuing logicist AI.
The last part of the class includes distinctive coverage of some of the great theorems of humanity’s greatest logician: Kurt Gödel.
- Terminology
Note that sometimes ‘symbolic’ is used in place of ‘formal.’ This is bad practice, since formal logic includes heterogeneous logics in which not only symbolic, but also pictorial information, figures. Deductive formal logic is a superset of mathematical logic; the latter is the part of deductive formal logic devoted to the mathematical analysis of mathematics itself (which is why some also use the term ‘meta-mathematics’ to denote mathematical logic). Part of the present course is devoted to mathematical logic. The specific phrase used to describe what the student is principally introduced to in this class is: beginning deductive logic, advanced (BDLA); hence the title of our textbook (see below).
- What Next?
After this class, the student can proceed to the intermediate level in formal deductive logic, and — with a deeper understanding and better prepared to flourish — to various areas within the formal sciences, which are invariably based on formal logic, at least to a high degree. The formal sciences include e.g. theoretical computer science (e.g., computability theory, complexity theory, rigorous coverage of programming and programming languages), mathematics in all its traditional branches (analysis, geometry, topology, etc), decision theory, (economic) game theory, set theory, probability theory, etc. The class also serves as a stepping stone to further study of AI, of formal/theoretical computer science, and of logic programming.
- What is Formal Logic?
In general, formal logic is the science and engineering of reasoning,1 but even this supremely general description fails to convey the flexibility and enormity of the field. For example, the vast majority of classical mathematics can be deductively derived from a small set of formulae (including, e.g., ZFC set theory, which you’ll be hearing more about, and exploring) expressed in the particular formal logics known as ‘first-order logic’ (FOL = \(\mathscr{L}_1\)) and ‘second-order logic’ (= SOL = \(\mathscr{L}_2\)); you’ll also be hearing more about both of these logics as well. In addition, computer science emerged from and is in large part based upon logic (for peerlessly cogent yet non-technical coverage of this emergence, see C Glymour’s Thinking Things Through). Logic is indeed the foundation for all at once rational-and-rigorous intellectual pursuits. (If you can find a counter-example, i.e. such a pursuit that doesn’t directly and crucially partake of logic, S Bringsjord would be very interested to see it.)
- Context: A Research University
You have wisely decided to attend a technical research university, with a faculty-led mission to create new knowledge and technology in collaboration with students. RPI is the oldest such place in the English-speaking world; it may know a thing or two about this mission. The mission drives those who teach you in this class. The last thing we want to do is simply convey to you how others present and teach introductory formal logic. As should be obvious by now, we think we have invented a better way to define, specify, and present formal logic, and are working hard to explain this invention, to explain it to others, and to disseminate the invention in question. The better way in question is denoted by the phrase ‘Logic: A Modern Approach\(^{TM}\),’ or simply by the abbreviation ‘LAMA\(^{TM}\),’ pronounced so as to rhyme with ‘llama.’
- A Disclaimer!
Please note that guest lecturers other than NS Govindarajulu and A Bringsjord should not be assumed to have fully affirmed the LAMATM paradigm. This thus applies specifically to TAs Aayush Masheshwarkar and Hariharan Sreenivas. As to what these thinkers hold in connection with LAMATM, that is an open question. You are free to inquire!
- Graduate Teaching Assistants; Further Help
The TAs for this course are the most-capable duo of Aayush Masheshwarkar and Hariharan Sreenivas; their email addresses, resp., are
aayushnmaheshwarkar@gmail.comandharhara4698@gmail.com. Please note again the subsection A Disclaimer!. - Prerequisites
There are no formal prerequisites. However, as said above, this course covers formal logic, and though the course is an introduction, it has also been said above that it’s an advanced, accelerated one. This implies that — for want of a better phrase — students are expected to have a degree of logico-mathematical maturity, achieved for example through mastery of first-rate coverage of high-school mathematics. You have this maturity and mastery on the assumption that you understood the math you were supposed to learn in order to make it where you are. For example, to get to where you are now, you were supposed to have learned the technique of indirect proof (= proof by contradiction = reductio ad absurdum), from either or both of the courses Algebra 2 and Geometry. An example of the list of concepts and techniques you are assumed to be familiar with from high-school geometry can be found in the common-core-connected Geometry: Common Core by Bass et al., published by Pearson in 2012. An example of the list of concepts and techniques you are assumed to be familiar with from high-school Algebra 2 can be found in the common-core-connected Algebra 2: Common Core by Bellman et al., published by Pearson, 2012. It’s recommended that during the first two weeks of the class, students review their high-school coverage of formal logic. While this material will be covered from scratch in this class, it helps to have at least some command of it from high school, since our pace will be a rapid one. A much more robust treatment of prerequisites and a suitable background for this course is provided in the syllabus.
Texts/Readings
Students will purchase access to and obtain the inseperably interconnected trio of
- the e-text Logic: A Modern Approach; Beginning Deductive Logic via HyperSlateTM, Advanced (LAMA-BDLA);
- the HyperSlateTM software system for (among other things) proof construction in collaboration with AI technology; and
- HyperGraderTM, an AI-infused online system for assessing, tracking, and broadcasting (in anonymized form on leaderboards) student progress.
Each member of this trio will be available online after purchase of the relevant code-carrying envelope in the RPI Bookstore. Full logistics of this purchase, and the content of the envelope and how to proceed from this content, will be explained the first class (and subsequently, as needed). Updates to LAMA-BDLA, and additional exercises, will be provided by listing on relevant LAMATM web pages upon signing in (and sometimes by email) through the course of the semester. You will need to manage many electronic files as this course proceeds, and e-housekeeping and e-orderliness are of paramount importance. You will specifically need to assemble a library of completed and partially completed proofs so that you can use them as building blocks in harder proofs; in other words, building up your own “logical library” will be crucial.
Please note that HyperSlateTM is
copyrighted: copying and/or distributing this software to others is strictly prohibited. You will need to AGREE online (after registration) a License Agreement. This agreement will also cover the textbook, which is copyrighted as well, and cannot be copied or distributed in any way, even in part.
In addition, occasionally papers may be assigned as reading. Two, indeed, were assigned in the syllabus, on the first day of class.
As to AI, it’s strongly recommended that students read the online summary of AI provided by Bringsjord & Govindarajulu, available here.
Finally, slide decks used in class will contain crucial additional content above and beyond LAMA-BDLA, information posted on HyperGraderTM, and on HyperSlateTM; this additional content will be available on the web site as the course unfolds through time.
Syllabus
The version of the course now underway is the Spring 2020 edition, the syllabus for which is available here. This is a robust, detailed syllabus, and is required reading — and reading that will pay off, for sure.
HyperSlateTM
This is the software system used for constructing proofs and arguments in collaboration with AI technology, and is available here after registration and sign-in.
HyperGraderTM
This is the AI system for submitting, getting assessed, and earning points for proofs and arguments constructed in HyperSlateTM, and is available here after registration and by sign-in.
LAMA-BDLA Textbook
This is the textbook for the course, and is obtained after registration and sign-in, by downloading.
Lectures
- January 13 2020: General Orientation to the LAMA\(^{TM}\) Paradigm, Logistics, Mechanics. (S Bringsjord)
The syllabus was projected and presented, and discussed, in detail. Please note that the syllabus, in particular, makes clear that students who wish to opt for learning under a different paradigm than that of LAMATM should take Intro to Logic in a Fall semester, since the “Stanford paradigm” is in use then.
- January 16 2020: Motivating Paradoxes, Puzzles, and \(\mathcal{R}\), Part I (a.k.a. “Why Study Logic?”; S Bringsjord)
The many answers to the “Why study formal logic?” question are enumerated, and explained. An avowal of Bringsjord’s immaterialist position on formal logic is included. For a full video of the 2018 version of this session done in 1:1 style, replete with audio proofs of some of the rather tricky problems presented, click here. Students for whom the problems presented are a breeze, can conceivably test out of the course, but one specific requirement in that regard is that such a student must’ve arrived from high school math and/or computer science with full command of explosion [viz. ∀ Φ, φ, ψ: if Φ \(\vdash\) φ ∧ ¬ φ, then Φ \(\vdash\) ψ].
- January 21 2020: MLK Day!
No class.
- January 23 2020: Motivating Paradoxes, Puzzles, and \(\mathcal{R}\), Part II (S Bringsjord)
This slide deck, expanded over that used in the previous class, shows some of solutions expressed as informal proofs, and contains Moriarty’s ticking-bomb challenge! — and also Special Llamas Disjunction.
- January 27 2020: Whirlwind History of Logic — With Skepticism About The Singularity Derived Therefrom (S Bringsjord)
In our time-traveling tour of computational formal logic and AI, we go from Euclid, three centuries BC, to — possibly? — The Singularity in our future, and along the way note that Leibniz, peerless polymath and autodidact, is the inventor of modern formal logic, and that at AI’s DARPA-sponsored dawn in 1956, the automated reasoning Logic Theorist stole the show. The presentation ends with Bringsjordian skepticism about The Singularity in light of (Turing-level) machine impotence in the face of the Entscheidungsproblem.
- January 30 2020: Propositional Calculus I (S Bringsjord)
This class meeting introduces one of the central tenets of LAMA\(^{TM}\): viz., that making immediate and continuous use of AI in the form of provabiity oracles (here, at the level of the propositional calculus) is indispendable for discovering valid proofs that solve problems. Examples using one of HyperSlate\(^{TM}\)’s oracles are given. The upshot is that proof discovery is a joint and indeed collaborative enterprise that unites superior human intelligence with inferior but invaluable machine intelligence.
- February 3 2020: Propositional Calculus II (S Bringsjord)
The simple but cornerstone inference rule of modus ponens (a.ka. /conditional elimination) is introduced, and claimed to be an element of the immaterial universe of of formal logic. This class meeting also introduces the powerful and — at least when it comes to precise, verifiable, valid reasoning — ubiquitous proof technique proof by cases, which in HyperSlate\(^{TM}\) corresponds to disjunction elimination. Tutorials are provided via real-time use of HyperSlate\(^{TM}\) on key exercises.
- February 6 2020: Propositional calculus III: Reductio ad Absurdum Proofs (S Bringsjord)
A crucial class, in which, harkening back to the astounding Euclid, we look at his still-edifying indirect proof that there must be infinitely many prime numbers, visit Algebra 2 from high school and note that in decent textbooks at this level there is in fact excellent coverage of indirect proof, and then see how reductio ad absurdum is regimented in HyperSlate.
- February 10 2020: Pure General Logic Programming (PGLP)
Every proof in HyperSlate, from the tiny to the elaborate, can be viewed as a Pure General Logic Programming (PGLP) program, and starting from an explanation of this fact, PGLP was presented, in its historical context.
- February 13 2020: The Pure Predicate Caclulus = \(\mathscr{L}_0\); Toward Quantification (Selmer Bringsjord)
We begin by noting that formal logic provides a way of seeing, contra Darwin (in Descent of Man), that H. sapiens sapiens is qualitatively distinct, intellectually speaking, from nonhuman animals, in light of the former’s ability to reason (1) with abstract relations and functions, (2) with quantifiers, (3) recursively, and (4) over and with infinite structures. The pure predicate calculus = zeroth-order logic = \(\mathscr{L}_0\) is introduced specifically in connection with (1), which, in contrast to the weaker propositional calculus = \(\mathscr{L}_{pc}\), it regiments and allows.
- February 20 2020: Quantification; FOL I; “Proving” God’s Existence (S Bringsjord)
Here begins coverage of \(\mathscr{L}_1\). We begin by noting the need for quantification in some very simple arguments, then explicitly introduce the two simplest inference rules/schemata for quantifiers in \(\mathscr{L}_1\). This meeting starts our coverage of the long-inseparable link between formal logic and purported proofs of God’s existence. We start with two such “proofs,” neither of which is intended to be taken seriously, but both of which have pedagogical value. Along the way we note that a serious series of purported proofs of God’s existence have been given by Anselm, Descartes, Leibniz, and — in the 20th century — by the greatest logician so far: G$\"{o}$del. Analysis of Gödel’s proof will need to wait for a later date; it’s by the way analyzed in a chapter in Bringsjord’s forthcoming Gödel’s Great Theorems, from Oxford University Press.
- February 24 2020: FOL II (Including
universal intro) (S Bringsjord)After the new inference schema
universal introis introduced, we end with some excercises that require putting it into action to reach some theorems (including three regarding the relative smartness of different Scandinavian countries). - February 27 2020: FOL III (existential elim); Logic, AI, Games, and the (Powerful!) Human Mind (S Bringsjord)
We first visit a ranking of the “hardness” of problems for humans and AIs based on formal logic. Next, the fourth and final new inference schema for FOL,
existential elim, is covered. In addition, after setting context by reviewing AI’s unimpressive victories in checkers, chess, Jeopardy!, and Go, some remarks are made on the nature of grid-based logic-puzzle games; specifically, it’s pointed out that when such games are played without obtaining proofs for the moves made by the player, the efficacy of such games, learning-wise, is questionable. - March 2 2020: Exhortation; Truth Trees; Measuring Human/Machine Intelligence; and FOL IV (S Bringsjord)
Truth trees are introduced, their superiority over truth tables is explained, and it’s shown that HyperSlate easily allows for the construction and testing of truth trees — in the very same environment used for the construction and testing of formal hypergraphical proofs. A challenge to Singularity-affirming thinkers, in the form of a very humble QAJ problem involving numerical quantification, is issued. This challenge comes after coverage of the basic machinery of this quantification, directly related to a relevant section in the LAMA-BDLA textbook.
- March 5 2020: Gödel’s Completeness Theorem (S Bringsjord)
Due to COVID-19, starting on this date, lectures are online. The link immediately above only goes to the slide deck in pdf form. The lecture itself, as a pair of videos, replete with some use of HyperSlateTM, is available in two parts: Part 1 and Part 2. After setting some context with a brief overview of G\"{o}del’s life, and the peerless collection of his greatest theorems (each of which is covered in the forthcoming G\"{o}del’s Great Theorems (by S Bringsjord; Oxford University Press), we cover the first of these theorems, which was achieved in G\"{o}del’s dissertation. This is G\"{o}del’s Completeness Theorem, and as part of it, K\"{o}nig’s Lemma (which G\"{o}del proved from scratch even though it has previously been proved); the theorem: Either (formula) \(\phi\) is satisfiable, or it’s refutable (here the formula is in FOL = \(\mathscr{L}_1\)).
- Spring Break
(Technically, the break was extended, but since IFLAI is largely self-paced and online via HyperGraderTM, that extension wasn’t impactful.)
- March 16 2020: The Liar; Russell’s Paradox; (Toward) Thoraf’s Paradox (S Bringsjord)
We here introduce our first paradox, perhaps the primogenitor: The Liar. Then we proceed to Russell’s Paradox, including the Norwegian barberesque version of it, which will soon be a Required Problem on HyperGraderTM. In fact, we take a look at two forthcoming problems in HyperSlateTM,
ChimericalBarber, and the problem that asks you to create the proof that Russell mailed Frege, and left a large part of the latter’s work in shambles as a result. Finally, we consider two problems that pave the way toward (Thoraf) Skolem’s Paradox (which we don’t directly engage). The lecture is available in its entirety in video form here. - March 19 2020: Rebuilding the Foundations of Math via ZFC; ZFC to Axiomatized Arithmetic (S Bringsjord)
After a quick review of the damage done by Russell’s Paradox, we present and discuss the fascinating and fiendishly clever Richard’s Paradox, which joins with Russell’s Theorem in destroying naïve set theory (including specifically Frege’s Axiom V). Then we take a look for the first time at Zermelo-Franenkel set theory (= ZFC), which saves the day when substituted for Frege’s axiomatization, and we specifically take a look at the Axiom Schema of Separation in ZFC. We end by taking a look at the first part of classical mathematics that can now be confidently built out from the foundation of ZFC: elementary arithmetic. The lecture is available in its entirety in video form here.
- March 23 2020 Test 2 (of course via HyperGraderTM)
One of the five, to be released on March 28, is a peronalized problem automatically generated, a unique problems for each student. Another one of the five is a problem of a new type: it asks the student to created his/her own problem, and measures the problem based on how difficult it is for the background AI to discover a proof that cracks the problem.
- March 26 2020: Astrologic; Second-Order Logic and the k-order Ladder; Second-Order Axiomatized Arithmetic; G\"{o}del’s God Theorem and Speedup Theorem (S Bringsjord)
This class introduces a fair amount of (important) formal logic unfortunately rarely seen at the introductory level. First, the novel concept of astrologic is introduced. Next, not only is second-order logic (SOL = \(\mathscr{L}_2\)) introduced, but the general method for climbing the higher-order-logic ladder is presented. This ladder of course reaches to \(\mathscr{L}_3\), and two specific connections to this logic (third-order logic, TOL) are discussed: The screenplay Double-Minded Man (an academic analysis of which, in connection with modern computational cognitive modeling, is given here), and Gödel’s ingenious proof of God’s existence, which he built atop Leibniz’s proofs, which in turn improved upon Descartes’ ontological proof of God’s existence. The video lecture is available here.
- March 30 2020: Devoted to tutorials only. (S Bringsjord)
- April 2 2020: Modal Logic: First Steps (S Bringsjord)
The main thrust of this lecture, available here, is to introduce the (propositional) modal logics K, T = M, D, S4, and S5. Specifically:
- We revist the “The Universe of Logic” diagram, and before moving to modal logic, introduce the infinitary first-order logic \(\mathscr{L}_{\omega_1 \omega}\), which is shown in the “Infinitary” category of logics in the diagram.
- We next explain the fundamental divide between extensional versus intensional logics, which is also shown in the diagram.
- With this divide in hand, we proceed to quickly introduce the five modal logics ranging from K to S5.
- April 6 2020: Standard Deontic Logic (SDL = D) Isn’t Going to Cut It! (Chisholm’s Paradox; The Free Choice Permission Paradox) (S Bringsjord)
In this lecture, to first show why we would want to consider a computational deontic logic in the first place, we quickly look at the threat posed by AIs that are at once powerful, autonomous, and intelligent, and conclude that these machines are dangerous. This is what I have dubbed “The PAID Problem.” We also quickly introduce the RAIR Lab’s proposed solution, in the form of The Four Steps. But The Four Steps solution requires for its basis a computational logic that can capture ethical theories and codes, as well as legal theories and codes. We introduce and discuss as a candidate logic for this, so-called Standard Deontic Logic (SDL) = D = M, which is now available in HyperSlateTM. Unfortunately, two paradoxes (from among many) lead us to reject D, and return to the drawing board, PAID still a looming threat.
- April 9 2020: Logic Can Save Us (Selmer Bringsjord & Naveen Sundar G & Atriya Sen)
Replete with robot demos, in this “Logic Can Save Us” lecture Selmer Bringsjord provides the RAIR Lab’s solution to the PAID Problem (and along the way briefly discusses another existential threat, that of pandemics), one that makes use not of a deficient deontic logic like D, but rather \(\mathcal{DCEC}^\ast\). Demos are shown. The presentation concludes with the robot version of the “Jungle Jim” moral dilemma, which demands moral creativity in machines.
- April 13 2020 Podcast on The Lovelace Test, AI, and Creativity
Something rather different is given here, in alignment with the HyperGraderTM Bonus Problem CreativityOpp1: a recent MindMatters podcast with Selmer Bringsjord, the pivot for the discussion being The Lovelace Test (of AIs), in honor of, and inspired by, Ada Lovelace, and the objection from her against Turing and his (misplaced) confidence that computing machines should be classified as genuinely thinking things when they can converse with humans under certain conditions.
- April 16 2020: The Lottery Paradox, Solved; and Introduction to /In/ductive Logic (S Bringsjord)
In this lecture, S Bringsjord’s provides a superior solution to the Lottery Paradox, by introducing a multi-valued inductive logic that does the trick, lickety split.
- April 20 2020: Gödel’s First Incompleteness Theorem (S Bringsjord; extracted from his Gödel’s Great Theorems)
This lecture covers the theorem for which Gödel is celebrated in the semi-popular literature and media; it says that, unfortunately, mathematics, indeed even just elementary arithmetic, contains an infinite number of propositions that will remain mysterious forever: unproved, with negations unproved as well (unless we turn to infinitary techniques). You have what you need to fully understand the theorem and proof, but if you are a mere mortal, will need to have your thinking cap on, and to be ready to pause the video as needed.
- April 23/30 2020 Final IFLAI 2020 Lecture: Could AI Ever Match Gödel’s Greatness? (S Bringsjord; partially based on th final chapter his Gödel’s Great Theorems)
In this lecture, the final one in IFLAI 2020, we explore the possibility of AI so powerful that it can reach Gödelian heights. Our investigation of this possibility includes reflection up a profound Either/Or proposition that Gödel introduced in a 1951 lecture at Brown University: either we are infinitely more powerful than any finite computing machine (e.g. a standard Turing machine), or else there are absolutely (human-)unsolvable Diophantine problems. The lecture ends with the AI vs. Gödel “Scorecard.”
Tutorials
- Getting Started with HyperGraderTM/HyperSlateTM
A simple tutorial, available here, in which someone signs in into HyperGraderTM and proves that switching the order of conjuncts is provable in the propositional calculus = \(\mathscr{L}_{PC}\).
- Thwarting Dr M’s Fiendish Challenge
The AI in HyperSlateTM is used here to confirm that the blue wire is the right one to snip, in order to save life on Earth.
- LoveyDovey: Exercise in Simple, Two-Level Quantification
The AI oracles of HyperSlateTM are used here to explore quantification at the two-layer level. The underlying file itself is available to registered students for their own exploration ad self-testing on HyperGraderTM (Exercise:
LoveyDovey). - Quick Goal-Analysis Progress on
FregTHEN2Leveraging chiefly the fact that
conditional introlives up to its name, I reduce this challenge to no more than modus ponens in short order, as shown here. - An AI-Based Proof Plan-Sketch for
KnightKnaveSmullyanKKProblem1.1By calling repeatedly on the AI at our disposal in HyperSlateTM, I craft a proof plan-sketch for the problem in question, as shown in the video available here.
- An AI-Based Proof Plan-Sketch for
QuantifierShift1There are other ways to crack this problem, but the plan-sketch given in this video seems to make a lot of sense, and certainly does indicate one route to a solution.
Pop Problems
These problems are presented in class in the absence of any preceding announcement that they are coming. Please see the syllabus for more information.
Homeworks
Homework consists of solving all required problems listed on HyperGraderTM’s web pages. (Non-required problems are clearly marked as such, e.g. as Bonus Problems.) All solutions are created in their final form in HyperSlateTM. HyperGraderTM for interactive use via its underlying AI technology opens for its Spring 2020 stint on or about Jan 27 2020, and an orientation/introduction to the system is given in class that day. Note that homeworks cannot be done without access to, and sustained and continuous use of, HyperSlateTM and HyperGraderTM.
Tests
There are three tests, each presented and taken via HyperGraderTM. Please see the syllabus for their dates.
Footnotes:
Warning: Increasingly, the term ‘reasoning’ is used by some who don’t really do anything related to reasoning, as traditionally understood, to nonetheless label what they do. Fortunately, it’s easy to verify that some reasoning is that which is covered by formal logic: If the reasoning is explicit; links declarative statements or formulae together via explicit, abstract reasoning schemata or rules of inference (giving rise to at least explicit arguments, and often proofs); is surveyable and inspectable, and ultimately machine-checkable; then the reasoning in question is what formal logic is the science and engineering of. (An immediate consequence of the characteristics just listed is that AIs based on artificial neural networks don’t reason, ever.) In order to characterize /in/formal logic, one can remove from the previous sentence the requirements that the links must conform to explicit reasoning schemas or rules of inference, and machine-checkability. It follows that so-called informal logic would revolve around arguments, but not proofs. An excellent overview of informal logic, which will be completely ignored in this class, is provided in “Informal Logic” in the Stanford Encyclopedia of Philosophy. In this article, it’s made clear that, yes, informal logic concentrates on the nature and uses of argument.