Introduction to (Formal) Logic (and AI) Spring 2023 Edition of IFLAI1 (“eye” • “fly” • “one”) Selmer Bringsjord
Table of Contents
with Naveen Sundar G.
∧ KB Foushée ∧ \(\ldots\)
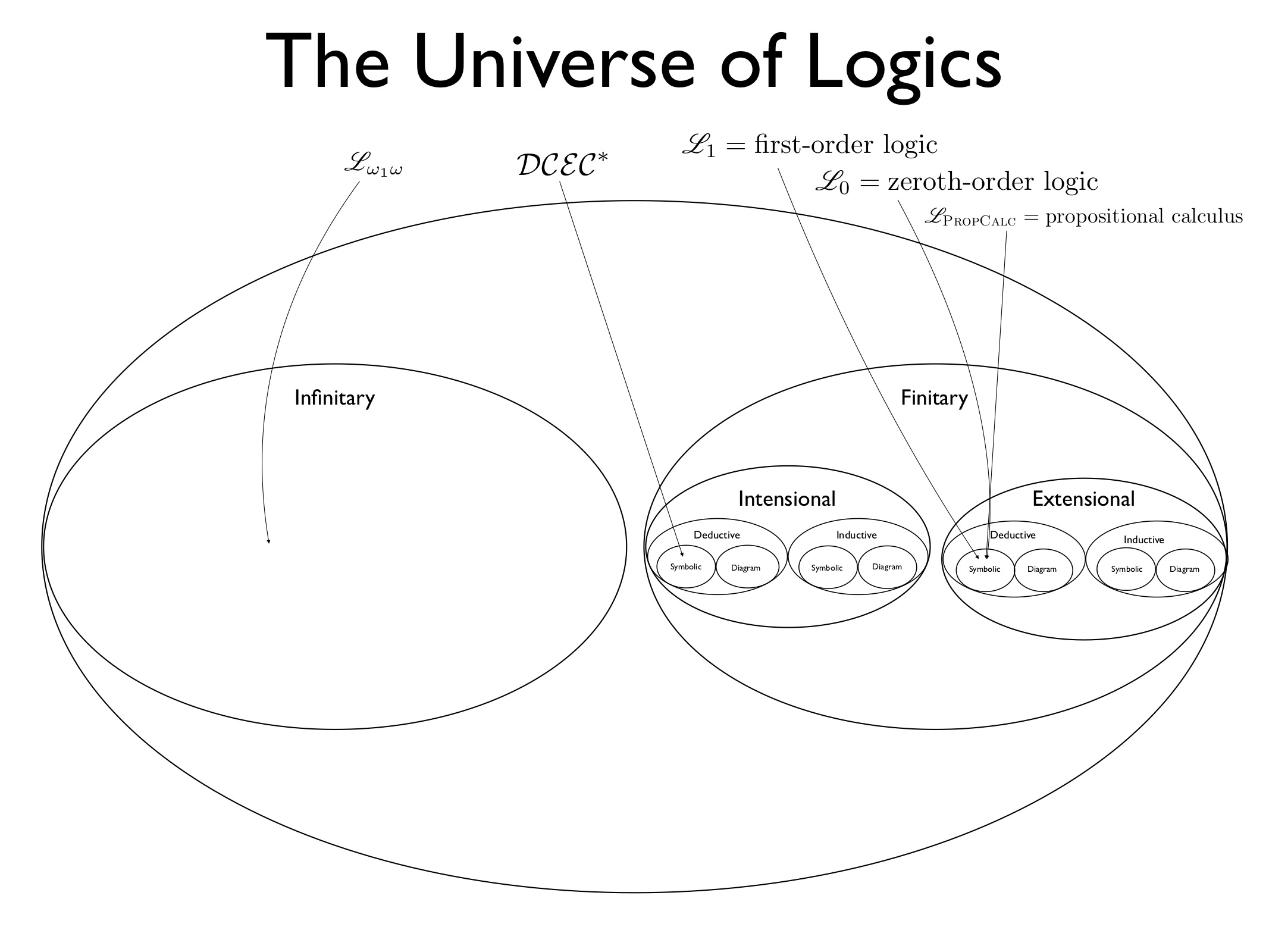

Figure 2: Larry

Figure 3: Lucy
[All artwork (all of which is copyrighted) for the LAMA® paradigm by KB Foushée.]
Terminology & General Orientation
This course is an advanced, accelerated introduction to deductive formal logic, with some substantive coverage of inductive formal logic, in which formalisms for dealing with uncertainty (e.g., probability theory, and also the likelihood calculus) are included, and to heterogeneous formal logic (which allows reasoning over not only textual/linguistic content, but visual content as well). The course conforms to the LAMA® paradigm in general, and is specifically based on *Hyperlogic*TM, which among other things (all of which are explained and covered) is based on the view that proofs and arguments are best cast as hypergraphs. Since the present course emphasizes deduction, the course is specifically based on hypergraphical natural deduction. This is the only robust treatment of formal logic based on this form of deduction, which has many unique advantages.
The course makes crucial use of patented AI for learning, and also provides an introduction to AI itself, at least AI of the logicist variety. In particular, and for example, students are exposed to a pure and general form of logic programming (so-called PGLP) that is particularly well-suited for pursuing logicist AI; students are also introduced to the new PGLP programming environment *Hyperlog*®. In addition, students are educated about the part of AI known as automated reasoning, which in general consists in AI itself reasoning in both deductive and inductive fashion.
The last part of the class includes distinctive coverage of some of the great theorems proved by humanity’s greatest logician: Kurt Gödel.
- Terminology
Note that sometimes ‘symbolic’ is used in place of ‘formal.’ This is bad practice, since formal logic includes heterogeneous logics in which not only symbolic, but also pictorial information, figures. Deductive formal logic is a superset of mathematical logic; the latter is the part of deductive formal logic devoted to the mathematical analysis of mathematics itself (which is why some also use the term ‘meta-mathematics’ to denote mathematical logic). Part of the present course is devoted to mathematical logic. The specific phrase used to describe what the student is principally introduced to in this class is: beginning deductive logic, advanced (BDLA); hence the title of our textbook (see below).
- What Next?
After this class, the student can proceed to the intermediate level in formal deductive and inductive logic, and — with a deeper understanding and better prepared to flourish — to various areas within the formal sciences, which are invariably based on formal logic, at least to a high degree. The formal sciences include e.g. theoretical computer science (e.g., computability theory, complexity theory, rigorous coverage of programming and programming languages), mathematics in all its traditional branches (analysis, geometry, topology, etc), decision theory, (economic) game theory, set theory, probability theory, etc. The class also serves as a stepping stone to further study of AI, of formal/theoretical computer science, and of in-depth logic programming.
- What is Formal Logic?
In general, formal logic is the science and engineering of reasoning,1 but even this supremely general description fails to convey the flexibility and enormity of the field. For example, the vast majority of classical mathematics can be deductively derived from a small set of formulae (including, e.g., ZFC set theory, which you’ll be hearing more about, and exploring) expressed in the particular formal logics known as ‘first-order logic’ (FOL = \(\mathscr{L}_1\)) and ‘second-order logic’ (= SOL = \(\mathscr{L}_2\)); you’ll also be hearing more about both of these logics as well. In addition, computer science emerged from and is in large part based upon logic (for peerlessly cogent yet non-technical coverage of this emergence, see C Glymour’s Thinking Things Through). Logic is indeed the foundation for all at once rational-and-rigorous intellectual pursuits. (If you can find a counter-example, i.e. such a pursuit that doesn’t directly and crucially partake of logic, S Bringsjord would be very interested to see it.)
- Context: A Research University
You have wisely decided to attend a technical research university, with a faculty-led mission to create new knowledge and technology in collaboration with students. RPI is the oldest such place in the English-speaking world; it may know a thing or two about this mission. The mission drives those who teach you in this class. The last thing we want to do is simply convey to you how others present and teach introductory formal logic. As should be obvious by now, Bringsjord thinks he has with others in Motalen invented a better way to define, specify, and present formal logic, and to use computational formal logic for AI, and he is toiling to explain this invention, to explain it to others, and to disseminate the invention in question. The better way in question is denoted by the phrase ‘Logic: A Modern Approach®,’ or simply by the abbreviation ‘LAMA®,’ pronounced so as to rhyme with ‘llama.’
- A Disclaimer!
Please note that guest lecturers other than NS Govindarajulu and A Bringsjord should not be assumed to have fully affirmed the LAMA® paradigm. This thus applies specifically to any and all TAs and graduate students. As to what these other thinkers hold in connection with LAMA®, that is an open question. You are free to inquire!
- Graduate Teaching Assistants; Further Help
The TA for this Sp 2023 edition of the course is Jeramey Tyler (
jerameytyler@gmail.com). Please note again the subsection A Disclaimer!. - Prerequisites
There are no formal prerequisites. However, as said above, this course covers formal logic, and though the course is an introduction, it has also been said above that it’s an advanced, accelerated one. This implies that — for want of a better phrase — students are expected to have a degree of logico-mathematical maturity, achieved for example through mastery of first-rate coverage of high-school mathematics. You have this maturity and mastery on the assumption that you understood the math you were supposed to learn in order to make it where you are. For example, to get to where you are now, you were supposed to have learned the technique of indirect proof (= proof by contradiction = reductio ad absurdum), from either or both of the courses Algebra 2 and Geometry. An example of the list of concepts and techniques you are assumed to be familiar with from high-school geometry can be found in the common-core-connected Geometry: Common Core by Bass et al., published by Pearson in 2012. An example of the list of concepts and techniques you are assumed to be familiar with from high-school Algebra 2 can be found in the common-core-connected Algebra 2: Common Core by Bellman et al., published by Pearson, 2012. It’s recommended that during the first two weeks of the class, students review their high-school coverage of formal logic. While this material will be covered from scratch in this class, it helps to have at least some command of it from high school, since our pace will be a rapid one. A much more robust treatment of prerequisites and a suitable background for this course is provided in the syllabus.
Texts/Readings
Students will purchase access to (and in the case of the e-textbook, obtain) the inseperably interconnected trio of
- HyperGrader®, a comprehensive, patented (Patent No. US 11,526,779 B2) AI platform generating, assessing, tracking, and broadcasting (in anonymized form on leaderboards) problems, the tackling of which largely takes place in
- the patented HyperSlate® AI system for (among other things) proof construction in collaboration with AI technology; and
- the (copyrighted) e-textbook Logic: A Modern Approach; Beginning Deductive Logic via HyperSlate®, Advanced (LAMA-BDLAHS).
Each member of this trio will be available online after purchase of the relevant code-carrying envelope from or in the RPI Follett Bookstore. Full logistics of this purchase, and the content of the envelope and how to proceed from this content, will be explained in the first class (and subsequently, in greater details, with walk-throughs given live). Updates to LAMA-BDLAHS, and additional exercises, will be provided by listing on relevant LAMA® web pages upon signing in to HyperGrader® (and sometimes by email) through the course of the semester. You will need to manage many electronic files as this course proceeds, and e-housekeeping and e-orderliness are of paramount importance. You will specifically need to assemble a library of completed and partially completed proofs in the cloud so that you can use them as building blocks in harder proofs; in other words, building up your own “logical library” will be crucial. This will be your library in HyperSlate®.
Please note that both HyperGrader® and HyperSlate® are both patented, copyrighted, trademarked AI systems; copying and/or reverse engineering or distributing this software to others is strictly prohibited by law. You will need to AGREE online (after registration) to a License Agreement. This agreement will also cover the e-textbook, which is copyrighted as well, and cannot be copied or distributed in any way, even in part.
In addition, occasionally papers may be assigned as reading. Two, indeed, were assigned in the syllabus, on the first day of class.
As to AI, it’s strongly recommended that students read the online summary of AI provided by Bringsjord & Govindarajulu, available here.
Finally, slide decks used in class will contain crucial additional content above and beyond LAMA-BDLA, information posted on HyperGrader®, and on HyperSlate®; this additional content will be available on the web site as the course unfolds through time.
Syllabus
The version of the course now underway is the Spring 2023 edition, the syllabus for which is available here. This is a robust, detailed syllabus, and is required reading — and reading that will pay off, for sure.
HyperSlate®
This is the patented intelligent software system used for constructing proofs and arguments in collaboration with AI technology, and is available after registration and sign-in.
HyperGrader®
This is the patented overarching AI platform (via which HyperSlate® is accessed) for submitting, getting assessed, and earning points for proofs and arguments constructed in HyperSlate®, and is available after registration and by sign-in.
LAMA-BDLAHS Textbook
This is the e-textbook for the course, and is obtained after registration and sign-in, by downloading fromm HyperGrader®.
Class-Day Content
- January 9 2023: General Orientation to the LAMA® Paradigm, Logistics, Mechanics. (S Bringsjord)
The syllabus was projected and presented, and discussed, in detail. Please note that the syllabus, in particular, makes clear that students who wish to opt for learning under a different paradigm and a different collection of software systems than that of LAMA® and its patented AI systems should take Intro to Logic in a Fall semester, since the “Stanford paradigm” is in use then.
- January 12 2023: The Immaterial Paradise; Motivating Paradoxes, Puzzles, and \mathcal{R}, Part I (a.k.a. “Why Study Logic?”; S Bringsjord)
The many answers to the “Why study formal logic?” question are enumerated, and explained. An avowal of Bringsjord’s immaterialist position on formal logic and human cognition is included. Students for whom all the problems presented are a breeze, can conceivably test out of the course, but one specific requirement in that regard is that such a student must’ve arrived from high school math and/or computer science with full command of explosion [viz. ∀ Φ, φ, ψ: if Φ ⊢ φ ∧ ¬ φ, then Φ ⊢ ψ], which is needed at a key juncture in this lecture.
- January 16 2023: MLK Day!
No class.
- January 19 2023: Motivating Paradoxes, Puzzles, Part II (S Bringsjord)
We first consider some “AI In The News”: whether AI’s should be conscious, as illogically argued in a recent NY Times opinion piece (“Without Consciousness, AIs Will Be Sociopaths,” Jan 13 2023). (Illogically? Yes: Contra the author, Princeton’s Prof. Graziano, from φ → φ one cannot validly deduce ¬ φ → ¬ ψ!) Next, after review of puzzlers involving boolean operators and the inference schema explosion, we then move to Moriarty’s fiendish ticking-bomb challenge! Can you solve it in time to save the world? Our last puzzler is the Monty Hall Problem (and an even-harder variant thereof), which requires both deductive and inductive logic to solve.
- January 23 2023: Whirlwind History of Logic — With Skepticism About The Singularity Derived Therefrom (S Bringsjord)
In our time-traveling tour of computational formal logic and AI, we go from Euclid, three centuries BC, to — possibly? — The Singularity in our future, and along the way note that Leibniz, peerless polymath and autodidact, is the inventor of modern formal logic, and that at AI’s DARPA-sponsored dawn in 1956, the automated reasoning Logic Theorist stole the show. The presentation ends with Bringsjordian skepticism about The Singularity in light of (Turing-level) machine impotence in the face of the Entscheidungsproblem.
- January 26 2023: Propositional Calculus I, Emphasis on Our First Oracle (S Bringsjord)
This class meeting introduces one of the central tenets of LAMA®: viz., that making immediate and continuous use of AI in the form of provabiity oracles (here, at the level of the propositional calculus) is indispendable for discovering valid proofs that solve problems. Examples using one of HyperSlate®’s oracles are given. The immediate upshot to note is that proof discovery is a joint and indeed collaborative enterprise that unites superior human intelligence with inferior but nonetheless invaluable machine intelligence in the form of automated reasoning.
- A video showing the use of the PC provability oracle in HyperSlate® solving the “NYS 3” logic problem is available here.
- January 30 2023: Propositional Calculus II (S Bringsjord)
The simple but cornerstone inference rule of modus ponens (a.k.a. conditional elimination) is introduced, and claimed to be an element of the immaterial universe of of formal logic. This class meeting also introduces the powerful and — at least when it comes to precise, verifiable, valid reasoning — ubiquitous proof technique proof by cases, which in HyperSlate® corresponds to disjunction elimination. Tutorials are provided via real-time use of HyperSlate® on key exercises.
- February 2 2023: Propositional calculus III: Reductio ad Absurdum Proofs (S Bringsjord)
A crucial class, in which, harkening back to the astounding Euclid, we look at his still-edifying indirect proof that there must be infinitely many prime numbers, visit Algebra 2 (and also Geometry) from high school and note that in decent textbooks at even this level there is in fact excellent coverage of indirect proof, and then see how reductio ad absurdum is formalized in HyperSlate®.
- February 6 2023: Pure General Logic Programming (PGLP), and Hyperlog, Part 1
Every proof in HyperSlate®, from the tiny to the elaborate, can be viewed as a Pure General Logic Programming (PGLP) program, and starting from an explanation of this fact (with some look-ahead discussion of the Turing-completeness of the first three elementary deductive logics covered in this class), PGLP, invented by S Bringsjord under support from both AFOSR and France’s ANR, is presented, in its historical context. This lecture also serves as a first introduction to the novel programming language and environment Hyperlog®; this new language is an instance of PGLP available in HyperSlate®, and is integrated with Clojure. In the second part of class, we review, in HyperSlate®, the propositional calculus = .
Selmer Bringsjord is inviting you to a Zoom-based office hour. Topic: Selmer Bringsjord's Office Hour Time: Feb 6, 2023 04:00 PM Eastern Time (US and Canada) Zoom meeting now expired.
- February 9 2023: Darwin’s Mistake+; The Pure Predicate Calculus = \(\mathscr{L}_0\); Toward Quantification (Selmer Bringsjord)
We begin by noting that formal logic provides a way of seeing, contra Darwin (in Descent of Man), that H. sapiens sapiens is qualitatively distinct, intellectually speaking, from nonhuman animals, in light of the former’s ability to reason (1) with abstract relations and functions, (2) with quantifiers, (3) recursively, and (4) over and with infinite structures. The pure predicate calculus = zeroth-order logic = \(\mathscr{L}_0\) is introduced specifically in connection with (1), which, in contrast to the weaker propositional calculus = \(\mathscr{L}_{pc}\), it regiments and allows. Presentation and discussion is rendered concrete by use of HyperSlate®.
- A full video lecture (earlier version), replete with explanation of the two new inference rules that distinguish zero-order logic from the mere propositional calculus, is available here.
- Zoom-mtg Info here:
Selmer Bringsjord is inviting you to a scheduled Zoom meeting. Topic: Selmer Bringsjord's Office Hour+ Time: Feb 9, 2023 04:00 PM Eastern Time (US and Canada) Zoom meeting now expired.
- February 13–21 2023: Test 1
Test 1 consists of six problems, two \(\mathscr{L}_{pc}\) problems of ascending difficulty (for the AI to solve), three \(\mathscr{L}_0\) problems of ascending difficulty (again, for the AI), and one human-authored problem (
tertium non datur).For some help, some solution videos for some earlier-year problems (in earlier, less-powerful versions of HyperSlate®) are given immediately below, but note that Selmer is here solving his own fourth problem, personalized just for him. One will learn a lot from watching these videos (and stopping and studying them along the way).
- The solution to the 2019 problem of showing \(\vdash_{L_{pc}} (A \rightarrow B) \rightarrow (B \rightarrow C) \rightarrow (A \rightarrow C)\) is available here.
- Phase 1 of the solution to EmmaHelpedToo, in which a proof-by-cases proof plan is created, is available here. EmmaHelpedToo was first presented in the “motivation” part (Part I) of the class; we have seen in class a valid informal proof that cracks this problem, and that prof is mapped into a formal correlate in HyperSlate®$, and expressed specifically as the proof-by-cases proof plan.
- The solution to one of Selmer’s personalized problems (from a few years back), which is rather “creative” on the part of the AI that produced it, is available here. As shown in the video, surisingly, three different routes are available for derving the GOAL from a subset of the GIVENs.
- Zoom-mtg Info here:
Zoom meeting has expired.
- February 16 2023: Quantification; FOL I; “Proving” God’s Existence (S Bringsjord)
Here begins coverage of \(\mathscr{L}_1\), and we thereby begin Part III of the course. We start by noting the need for quantification in some very simple arguments, then explicitly introduce the two simplest inference rules/schemata for quantifiers in \(\mathscr{L}_1\). This meeting starts our coverage of the long-inseparable link between formal logic and purported proofs of God’s existence. We start with two such “proofs,” neither of which is intended to be taken seriously, but both of which have pedagogical value. Along the way we note that a serious series of purported proofs of God’s existence have been given by Anselm, Descartes, Leibniz, and — in the 20th century — by the greatest logician so far: Gödel. Analysis of Gödel’s proof will need to wait for a later date; it’s by the way analyzed in a chapter in Bringsjord’s forthcoming Gödel’s Great Theorems, from Oxford University Press.
- A full (but in-the-past) video lecture, replete with explanation of the first two new inference rules/schemata for hypergraphical first-order logic, is available here.
- Zoom-mtg Info here:
Zoom meeting has expired.
- February 21 2023: The Gist of Soundness via Truth (Hyper)Graphs (S Bringsjord)
We explore the morphing of hypergraphical proofs into hypergraphs that subsume so-called “truth trees,” and with that done for some inference rules/schemata for ℒpc, we note that it can be done all in the same “morphing” manner, and that therefore soundness (essentially and informally put: provability implies a fully closed truth tree/graph in the corresponding case) is easy to prove.
Selmer Bringsjord is inviting you to a scheduled Zoom meeting. Topic: Z Mtg Office Hour+ Zoom meeting now ended.
- Feb 22 2023: FOL II (including
universal intro) (S Bringsjord)After the usual pointer to an AI-in-the-News issue, the new inference rule/schema
universal introis introduced, we move to HyperSlate® in order to bring to life a simple but esemplastic example. We end by looking at some excercises that require putting it into action to reach some theorems (including three regarding the relative smartness of different Scandinavian countries).Selmer Bringsjord is inviting you to a scheduled Zoom meeting. Topic: Selmer Bringsjord's Office Hour+ Time: Feb 23, 2023 04:00 PM Eastern Time (US and Canada) Zoom mtg ended.
- February 27 2023: FOL III (existential elim); Logic, AI, Games, and the (Powerful!) Human Mind (S Bringsjord)
We first visit a ranking of the “hardness” of problems for humans and AIs based on formal logic. Next, the fourth and final new inference schema for FOL,
existential elim, is covered. In addition, after setting context by reviewing AI’s unimpressive victories in checkers, chess, Jeopardy!, and Go, some remarks are made on the nature of grid-based logic-puzzle games; specifically, it’s pointed out that when such games are played without obtaining proofs for the moves made by the player, the efficacy of such games, learning-wise, is questionable. We also discuss Motalen’s latest game: LogiNim.- Zoom-mtg Info here:
Selmer Bringsjord is inviting you to a scheduled Zoom meeting. Topic: Selmer Bringsjord's Office Hour+ Zoom mtg has ended.
- March 2 2023: The Liar; Russell’s Paradox; (Toward, only) Thoraf’s Paradox (S Bringsjord)
We introduce our first paradox, perhaps the primogenitor of all paradoxes: The Liar Paradox, or just simply: The Liar. Next, we proceed to Russell’s Paradox, including the Norwegian barberesque version of it, which will soon be a Required Problem on HyperGrader®. In fact, we mention two forthcoming problems in HyperSlate®,
ChimericalBarber, and the problem that asks you to create the proof that Russell mailed Frege, and left a large part of the latter’s work in shambles as a result (RusselsLetter2Frege). Finally, we consider two problems that pave the way toward (Thoraf) Skolem’s Paradox (which we don’t directly engage).- Zoom-mtg Info here:
Zoom meeting now expired.
- Spring Break!
- March 13 2023: Rebuilding the Foundations of Math via ZFC; Baby Arithmetic (BA) and Peano Arithmetic (PA) (S Bringsjord)
After a quick review of the damage done by Russell’s Paradox, we present and discuss the fascinating and fiendishly clever Richard’s Paradox, which joins with Russell’s Theorem in destroying naïve set theory (including specifically Frege’s Axiom V). Then we take a look for the first time at Zermelo-Franenkel set theory (= ZFC), which saves the day when substituted for Frege’s axiomatization, and we specifically take a look at the Axiom Schema of Separation (SEP) in ZFC, and then look at SEP in HyperSlate®. We end by taking a look at the first part of classical mathematics that can now be confidently built out from the foundation of ZFC: elementary arithmetic, expressed in formal logic. Here we look at Baby Arithmetic (BA) and Peano Arithmetic (PA), and in the case of the former explore a new excercise in HyperGrader®.
- Zoom-mtg Info here:
Zoom meeting now expired.
- March 16 2023: Climbing the k-Order Ladder; God and Third-Order Logic; Astrologic (S Bringsjord)
We here bring a large swathe of our Universe of Logics to life, by moving beyond first-order logic (ℒ1) into second- and third-order logic, the latter a logic Gödel used for his famous proof of God’s existence. We end by considering so-called “Astrologic,” which is logic for all human-level beings, including those on other planets (if such exist).
- Zoom-mtg Info here:
Selmer Bringsjord is inviting you to a scheduled Zoom meeting. Zoom meeting now expired.
- March 20 2023 Test 2, Introduced and Explained (of course via HyperGrader®)
- Zoom-mtg Info here:
Zoom meeting now expired.
- March 24 2023 On to Intensional Logics
This is a general introduction, using the robot Blinky and a shell game, along with the False Belief task at level 5 and beyond, to the crucial difference between extensional logics versus intensional logics. The logics \(\mathscr{L}_{pc}\), \(\mathscr{L}_0\), \(\mathscr{L}_1\), \(\mathscr{L}_2\), \(\mathscr{L}_3\) are all extensional. Now we move to the intensional category, which includes modal logics. Six modal logics are introduced, rapidly for now: K, T = M, D, S4, S5, and \(\mathcal{DCEC}\). A first proof in K of its characteristic axiom is constructed in HyperSlate®.
- Zoom-mtg Info here:
Zoom meeting now expired.
- March 27 2023: Against Killer Robots, Standard Deontic Logic (SDL = D) Isn’t Going to Cut It! (Chisholm’s Paradox; The Free Choice Permission Paradox; Ross’s Paradox) (S Bringsjord)
In this lecture, to first show why we would want to consider a computational deontic logic in the first place, we quickly look at the threat posed by AIs that are at once powerful, autonomous, and intelligent, and conclude that these machines are dangerous. This is what I have dubbed “The PAID Problem.” We also quickly introduce the RAIR Lab’s proposed solution, in the form of The Four Steps. But The Four Steps solution requires for its basis a computational logic that can capture ethical theories and codes, as well as legal theories and codes. We introduce and discuss as a candidate logic for this, so-called Standard Deontic Logic (SDL) = D = M, which is available in HyperSlate®. Unfortunately, three paradoxes (from among many) lead us to reject D, and return to the drawing board, PAID still a looming threat.
- Zoom-mtg Info here:
Zoom meeting expired.
- March 30 2023: Logic Can Save Us (Selmer Bringsjord & Naveen Sundar G)
Replete with robot demos, in this lecture Selmer Bringsjord provides the RAIR Lab’s solution to the PAID Problem (and along the way briefly discusses another existential threat, that of pandemics), one that makes use not of the deficient deontic logic like D, but rather \(\mathcal{DCEC}^\ast\). Demos are shown. The presentation concludes with the robot version of the “Jungle Jim” ethical super-dilemma, which demands moral creativity in machines.
- Zoom-mtg Info here:
Zoom meeting now in the past.
- April 3 2023: Intro to Inductive Logic via The Monty Hall Problem, The Paradox of Grue, The Lottery Paradox, and AI for Drone Strikes (S Bringsjord)
We begin by making the crucial distinction between deductive logic versus inductive logic, and take note of the fact that we’ve been (and will again after today) learning the former, not the latter. We then review The Monty Hall Problem to see that for at least some applications/domains formal logic must include both deduction over bivalent propositions and some machinery to cover uncertainty values (e.g. probability values between 0 and 1). Next, we briefly visit The Paradox of Grue, which is solved in detail in Bringsjord’s intermediate logic-and-AI class (IFLAI2), in order to explain that this paradox serves to divide and define three fundamentally different approaches to formal inductive logic, one that originates in Carnap and is mathematical, traditionally non-computational, and not proof-/argument-based (pure inductive logic); one that is rooted in philosophy and informal argumentation/informal logic; and the third approach, the one pursued by S Bringsjord:
Base inductive logic on argument and proof, but do so in a formal/mathematical manner, and include not only probability theory and its relatives, but likelihood as well.
This third approach enables S Bringsjord to provide a superior solution to The Lottery Paradox, by introducing a multi-valued inductive logic based on likelihood values that does the trick, lickety split. We end with some discussion of AI based on computational inductive logic of the third type for enabling AI to make rational, ethical decisions about drone strikes.
- Zoom-mtg Info here:
Zoom Meeting now expired.
- April 6 2023: Overview of GGT Book; Gödel’s Completeness Theorem (S Bringsjord)
After setting some context with a brief overview of the peerless collection of Gödel’s greatest theorems (each of which is covered in the forthcoming Gödel’s Great Theorems (by S Bringsjord; Oxford University Press), we cover the first of these theorems, which was achieved in Gödel’s dissertation. This is Gödel’s Completeness Theorem, and as part of it, König’s Lemma (which Gödel proved from scratch even though it has previously been proved); the theorem: Either (formula) \(\phi\) is satisfiable, or it’s refutable (here the formula is in FOL = \(\mathscr{L}_1\)). It will be necessary to make use of hand-drawn content to allow some examples to be worked out; these examples involve a tree-based approach to establish satisfiability if doing so is possible; and reference to a deductive refutation of \(\phi\) if doing so is not possible.
- Zoom-mtg Info here:
Zoom meeting now in the past.
- April 10 2023: Gödel’s First Incompleteness Theorem (S Bringsjord; extracted from his Gödel’s Great Theorems)
This lecture covers the theorem for which Gödel is celebrated in the semi-popular literature and media; it says that, unfortunately, mathematics, indeed even just elementary arithmetic, contains an infinite number of propositions that will remain mysterious forever: unproved, with negations unproved as well (unless we turn to infinitary techniques: we assume that our axiom systems and our proof techniques are limited in certain ways — ways that yours truly, generally following Zermelo, rejects.) You have what you need to fully understand the theorem and proof, but if you are a mere mortal, will need to have your thinking cap on, and to be ready to ask questions as needed. To make things easier, I have come up with a single-paragraph, semi-formal proof that we cannot have a sentence that asserts its own unprovability.
- Zoom-mtg Info here:
Zoom meeting now expired.
- April 13 2023: Gödel’s Second Incompleteness Theorem (S Bringsjord)
We here cover Gödel’s second incompleteness theorem (G2), which is a corollary of G1. As a matter of fact, armed with the Fixed Point Theorem, and G1, G2 really is rather a piece of cake to prove!
- Zoom-mtg Info here:
Zoom meeting now irretrievably in the past.
- April 17 2023: Gödel’s Silver Blaze Theorem: $ZFC ¬\vdash ¬ CH (S Bringsjord)
We here cover Gödel’s Greatest Theorem, in which he shows that ZFC set theory doesn’t deductively entail the Continuum Hypothesis (CH). [We leave aside the Generalized CH (GCH).] Without making any use of transfinite numbers, we set out and reflect upon both CH and the GCH. We then analyze the reasoning of Sherlock Holmes in the The Adventure of Silver Blaze, which is fundamentally a proof of non-entailment in its own right (and shows Scotland Yard, once again, to be, well, not exactly a place of ingenious detection). Finally, we pass to presentation and explanation of a proof-sketch of Gödel’s stunning results (put informally) that mathematics can’t be used to prove mathematics free of contradiction.
- Zoom-mtg Info here:
Zoom meeting now in the past.
- April 20 2023: Gödel’s Time Travel Theorem (S Bringsjord)
We here look at the context, paradoxes related to and arising from, and diagrammatic justification for: Gödel’s birthday present to Einstein: a proof that backwards time travel in (Einstein’s) General Theory of Relativity is possible.
- Zoom-mtg Info here:
Zoom meeting now expired.
- April 24 2023 Final IFLAI 2023 Lecture: Could AI Ever Match Gödel’s Greatness? (S Bringsjord; based on Part II of final chap his Gödel’s Great Theorems)
In this lecture, the final one in IFLAI 2022, we explore the possibility of AI so powerful that it can reach Gödelian heights. Our investigation of this possibility includes reflection up a profound Either/Or proposition that Gödel introduced in a 1951 lecture at Brown University: either we are infinitely more powerful than any finite computing machine (e.g. a standard Turing machine, or the machines that underlie HyperSlate®), or else there are absolutely (human-)unsolvable Diophantine problems. The lecture (proper) ends with the AI vs. Gödel “Scorecard,” and then discussion of the number and type of problems in forthcoming Test 3, and the grading scheme thereof.
- Zoom-mtg Info here:
Selmer Bringsjord is inviting you to a scheduled Zoom meeting. Topic: Selmer Bringsjord's Office Hour+ Time: Apr 24, 2023 04:00 PM Eastern Time (US and Canada) Join Zoom Meeting https://us02web.zoom.us/j/87924286764?pwd=UTJ6Y1Z1N1V3endMaEtmendZZlRtQT09 Meeting ID: 879 2428 6764 Passcode: 721179
Tutorials (expands as semester unfolds)
- Getting Registered with HyperGrader®/HyperSlate®
A simple tutorial, available here, in which someone registers into HyperGrader® and proves that switching the order of conjuncts is provable in the propositional calculus = \(\mathscr{L}_{PC}\). This proof wins a trophy and earns a leaderboard spot for the Exercise
switching_conjuncts_fine. - Getting Started with HyperSlate®: Propositional Calculus
In this tutorial, available here, S Bringsjord starts from scratch with a blank workspace and uses HyperSlate® and the PC provability oracle available therein to show that the atomic proposition \(h\) can be deduced from \(\{\neg \neg c, c \rightarrow a, \neg a \vee b, b \rightarrow d, \neg (d \vee e)\}\). The main purpose of this video is coverage of the intuitive interface and basic moves therein.
Pop Problems
These problems are timed and released in HyperGrader® in the absence of any preceding announcement that they are coming. Please see the syllabus for more information.
Homeworks
Homework consists of solving all Required problems listed on HyperGrader®’s web pages. (Non-required problems are clearly marked as such, e.g. as Bonus Problems.) All solutions are created in their final form in HyperSlate®. HyperGrader® for interactive use via its underlying AI technology opens for its Spring 2023 stint on or about Jan 26 2023, and an orientation/introduction to the system is given in class that day. Note that homeworks cannot be done without access to, and sustained and continuous use of, HyperSlate®, access via the AI platform HyperGrader®.
Tests
There are three tests, each presented and taken online and outside of class via HyperGrader®. Please see the syllabus for their release dates.
Footnotes:
Warning: Increasingly, the term ‘reasoning’ is used by some who don’t really do anything related to reasoning, as traditionally understood, to nonetheless label what they do. Fortunately, it’s easy to verify that some reasoning is that which is covered by formal logic: If the reasoning is explicit; links declarative statements or formulae together via explicit, abstract reasoning schemata or rules of inference (giving rise to at least explicit arguments, and often proofs); is surveyable and inspectable, and ultimately machine-checkable; then the reasoning in question is what formal logic is the science and engineering of. (An immediate consequence of the characteristics just listed is that AIs based on artificial neural networks don’t reason, ever.) In order to characterize /in/formal logic, one can remove from the previous sentence the requirements that the links must conform to explicit reasoning schemas or rules of inference, and machine-checkability. It follows that so-called informal logic would revolve around arguments, but not proofs. An excellent overview of informal logic, which will be completely ignored in this class, is provided in “Informal Logic” in the Stanford Encyclopedia of Philosophy. In this article, it’s made clear that, yes, informal logic concentrates on the nature and uses of argument.